✅LAS INTEGRALES😄INTRODUCCIÓN 🔥(FACIL Y RAPIDO)⏳EN🔟MINUTOS

Llamaremos primitiva de una función  respecto de la variable , a una función  que cumpla que 

Es el proceso inverso a obtener la función derivada:

 Derivada: a partir de una función obtenemos su función derivada
 Primitiva: a partir de la función derivada obtenemos la función primitiva de la que procede

Si tenemos la función  podemos comprobar que una primitiva sería  (al derivar 5x obtenemos 5).
Pero también serían primitivas las funciones  , , , etc. (al derivar cualquiera de ellas obtendríamos 5).
Tendríamos infinitas primitivas de la forma  (siendo C una constante que podría representar cualquier número)

Llamaremos integral indefinida de f(x) al conjunto de todas las primitivas de dicha función y lo representaremos por:

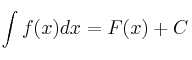
En la expresión anterior tenemos (de izquierda a derecha):
 : símbolo de integral
 : integrando (la función que queremos integrar)
 : diferencial de x (x es la variable respecto de la que queremos integrar)
 : primitiva
 : constante de integración

Integración: podemos llamar integración al proceso mediante el cual obtenemos la integral indefinida de una función. Para ello existen varios métodos:

 Integrales Inmediatas. Consiste en aplicar fórmulas de manera semejante al cálculo de derivadas.
 Integración por partes
 Integración por cambio de variable (o sustitución)
 Integración de funciones racionales
 etc.

  TE DEJO UN VIDEO SOBRE ESTE TEMA PARA QUE ENTIENDAS MEJOR